Detect All Stars Using CADE

I recently listened to David Jensen give a brief overview of an anomaly detection method called CADE or Classifier Adjusted Density Estimation. The method seemed very easy to grasp at first which is not usually the case for recently published machine learning work. I can never resist trying to implement these things myself on a toy example to learn what makes them tick and if they really deliver on what they promise.

I wanted to try to create an example that will find anomalous players in the NBA. I think in order to do this I may have to expand on some of the later steps of this methodology though. But first we need some data. Lets walk through the steps I am using to get this data.

Setup

I have a package on Github that we will utilize to get data. First we need to get this functionality installed. The code is actually very similar to some code I have used in previous posts except I realized some of the sites have changed and we only need a subset of that functionality.

require(plyr)
require(XML)
require(devtools)
require(randomForest)

install_github('darrkj/CadeAllStar')

require(CadeAllStar)

Before we proceed I should explain a bit more about what I am attempting to do here. I am hoping to find the best players in the league, All Stars, in order to do that I am going to try to find those which are the largest outliers. In doing this I may find some players that are not all stars but different for some other reason which will also be interesting. The methodology being used looks at player-days, statistics from a single game for a specific player. It then finds the player-games that are anomalous to the rest of the player-game population. My intuition tells me that I can aggregate these games up to the player level and have and ordering of players. Those that are the furthest out should contain the group of all stars, possibly including other groups of players as well. I will attempt to explain the details of the actual outlier detection method as it is needed.

# You can pull all data for the 2013 season via the following code.
season <- seasonify(2013)

# Or use the 2013 season that comes with the R package.
data(season)

head(season[, 1:3])

##                       away                home       date
## 72          Boston Celtics          Miami Heat 2012-10-30
## 269       Dallas Mavericks  Los Angeles Lakers 2012-10-30
## 1303    Washington Wizards Cleveland Cavaliers 2012-10-30
## 294       Dallas Mavericks           Utah Jazz 2012-10-31
## 335         Denver Nuggets  Philadelphia 76ers 2012-10-31
## 406  Golden State Warriors        Phoenix Suns 2012-10-31

Now we have an entire season of NBA games. This is still only the games though. We need to capture each players’ stats for each of these games. We are only going to pull the basic statistics. This will also take a while so I would recommend using the data in the package.

# Pull statistics for a season of games
stats <- pull_stats(season)

Or load it from the package.

data(stats)

head(stats[, 1:3])

##          player FG FGA
## 1   Rajon Rondo  9  14
## 2   Paul Pierce  6  15
## 3 Kevin Garnett  4   8
## 4  Brandon Bass  6  11
## 5  Courtney Lee  5   6
## 7   Jason Terry  2   7

Implement the Algorithm

Now on to the technical aspects. The heart of CADE relies on two things:

1. Creating uniform distributions over variables
2. Generate a classifier which can produce a probability

The following function takes care of the uniform distribution by taking a variable that may have any type of distribution and returns one with the same length and range but is uniformly distributed.

uni <- function(x, len = length(x)) {
  if ( is.integer(x) ) {
    sample(min(x):max(x), len, replace = TRUE)
  } else if ( is.numeric(x) ) {
    runif(len, min(x), max(x))
  } else if ( is.factor(x) ) {
    factor(sample(levels(x), len, replace = TRUE))
  } else {
    sample(unique(x), len, replace = TRUE)
  }
}

Here is how this looks for a Poisson distribution.

test <- rpois(10000, 35)
par(mfrow = c(2, 1))

hist(test)
hist(uni(test))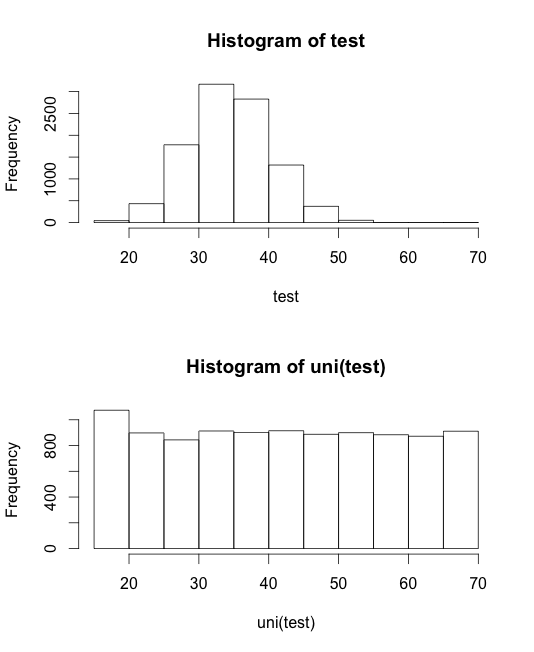

Now the rest of CADE is just about creating predictions. The predictions are of cases that are outliers. To do this we make a naive assumption that none of our data is an outlier. Thus we will create a new target variable y, and give it all values of 0. Then we need to take the fake uniform data that is structurally the same and give it the same target variable y but only call of the outliers so they get a value of 1. Then we combine these data sets into one and run a machine learning algorithm on them which is able to return a probability instead of a predicted class outcome. Then we use this classifier to evaluate our original data. We call this predicted probability the probability of being an outlier.

cade <- function(df, numTree = 500) {
  stopifnot(is.data.frame(df))

  # This is the data we will make the 'no' case
  real <- df
  
  # Create similar but uniform data
  fake <- as.data.frame(lapply(real, uni))
  
  real$y <- 0
  fake$y <- 1
  
  # Combine real and fake data
  data <- rbind(real, fake)
  
  # Build classifier
  tree <- randomForest(as.factor(y) ~ ., data = data, ntree = numTree)
  
  # The classifier probabilities
  df$prob <- predict(tree, newdata = df, type = 'prob')[, 2]
  df$prob <- df$prob / (1 - df$prob)
  
  df
}

Application

Everything is now in place to try out our experiment. We need to pass the data into the CADE function, only the fields that are needed though. Since the result of the function is a new data frame with a field called prob, we can just take take that field and assign it to the data we pass into the function.

# Run cade on data, this takes a minute, for analysis only use relevant fields.
stats$prob <- cade(subset(stats, select = -c(player, date, guid)))$prob

# Order by most likely to be an outlier.
stats <- stats[order(stats$prob, decreasing = TRUE), ]

# Do people appear in the top frequently.
rev(sort(table(stats$player[1:30])))

## 
##      Kevin Durant           James Harden       Kevin Love  
##                 7                 4                 3                 
##      Russell Westbrook      LeBron James       Kobe Bryant
##                 2                 2                 2 
##      Spencer Hawes          Paul Pierce        Paul George      
##                 1                 1                 1   
##      Nicolas Batum          Kyrie Irving       Josh Smith
##                 1                 1                 1 
##      John Wall              Jeff Green         Dwight Howard      
##                 1                 1                 1         
##      Byron Mullens        
##                 1

Even though it is somewhat subjective to as to who is better than who in the NBA, I think there would be little down that these are not some of the best players of 2013. How would these results line up against the actual 2013 Allstar Game?

First we have to find a way to get rid of player-game values and just get values based on player. I thought over just counts under some threshold but I could not think of any way to determine this threshold. It was all kind of arbitrary. Adding probabilities up is not something that commonly pops up. This may be okay here though, I know the sum is no longer any way a probability, some will rise above 1.

# Aggregate the per game score up to just the player
rank <- ddply(stats, .(player), summarise, score = sum(prob))

# Order largest sum
rank <- rank[order(rank$score, decreasing = TRUE), ]

# Rank each player by there sum total.
rank$rank <- 1:nrow(rank)
head(rank)

##              player score rank
## 266    Kevin Durant 7.668    1
## 191    James Harden 5.745    2
## 298    LeBron James 4.443    3
## 59  Carmelo Anthony 4.058    4
## 136   Dwight Howard 4.022    5
## 278     Kobe Bryant 3.938    6

This looks great

# Load all star game data
al2013 <- 'http://www.allstarnba.es/editions/2013.htm'
al2013 <- readHTMLTable(al2013)

# Join and clean these fields.
al2013 <- setdiff(c(al2013[[1]]$` EAST`, al2013[[2]]$` WEST`), 'TOTALS')

# Move all text to lower to be safe(er) in joining data.
al2013 <- data.frame(player = tolower(al2013))
rank$player <- tolower(rank$player)

# Join data
al2013 <- merge(al2013, rank)

# Order data by rank
al2013 <- al2013[order(al2013$rank), ]

# How far into the list do you need to go to capture the whole all star lineup
al2013$depth <- al2013$rank / nrow(rank)

al2013

##               player  score rank    depth
## 12      kevin durant 7.6682    1 0.002128
## 9       james harden 5.7449    2 0.004255
## 17      lebron james 4.4426    3 0.006383
## 3    carmelo anthony 4.0576    4 0.008511
## 7      dwight howard 4.0224    5 0.010638
## 14       kobe bryant 3.9376    6 0.012766
## 19       paul george 2.6216    7 0.014894
## 21 russell westbrook 2.3884    8 0.017021
## 10       joakim noah 1.4070   15 0.031915
## 22        tim duncan 1.3865   16 0.034043
## 8        dwyane wade 1.0168   21 0.044681
## 5         chris paul 0.9468   24 0.051064
## 2        brook lopez 0.8438   25 0.053191
## 16 lamarcus aldridge 0.7993   27 0.057447
## 15      kyrie irving 0.6615   34 0.072340
## 18         luol deng 0.6580   35 0.074468
## 25     zach randolph 0.6336   37 0.078723
## 11      jrue holiday 0.5908   40 0.085106
## 20       rajon rondo 0.5218   47 0.100000
## 1      blake griffin 0.4044   55 0.117021
## 4         chris bosh 0.3317   67 0.142553
## 24    tyson chandler 0.2165   89 0.189362
## 6          david lee 0.2083   92 0.195745
## 13     kevin garnett 0.1961   95 0.202128
## 23       tony parker 0.1893   97 0.206383